Теоретический материал к задаче 1 типа
Значение производной функции f(x) в точке
xo равно tga — угловому коэффициенту
касательной,
проведенной к графику этой функции в данной точке. Чтобы найти угловой
коэффициент, выберем две точки А и В, лежащие на касательной, абсциссы и
ординаты
которых — целые числа. Теперь определим модуль углового коэффициента.
Для этого
построим прямоугольный треугольник ABC, где
АВ является
гипотенузой. Важно
помнить, что тангенс острого
угла прямоугольного
треугольника — это отношение
противолежащего катета к прилежащему.
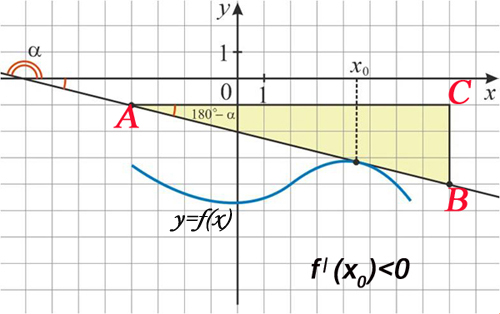
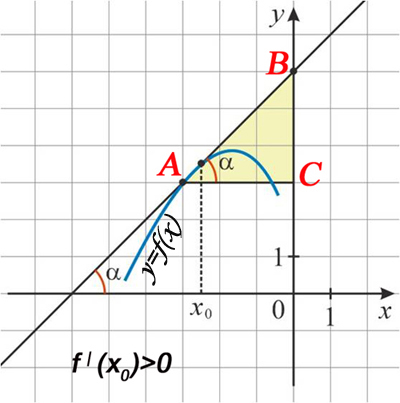
Знак производной (углового коэффициента)
можно определить по рисунку,
например, так: если касательная составляет с положительной
полуосью ОХ острый угол,
то производная положительна,
если касательная составляет с
положительной полуосью ОХ тупой угол - отрицательна
(если касательная параллельна
оcи OX, то производная равна нулю).
|