Теоретический материал к задаче 7 типа
Если функция y=f(x) имеет экстремум в точке xo,
то в этой точке производная функции либо
равна нулю, либо не существует.
Заметим, что при переходе через точку максимума изменяется характер монотонности функции:
слева от точки максимума функция возрастает, справа – убывает. Следовательно, изменяются
знаки
производной: слева от точки максимума производная положительна, справа -
отрицательна.
При переходе через точку минимума также изменяется характер монотонности функции:
слева
от точки минимума функция убывает, справа – возрастает. Следовательно, изменяются знаки
производной: слева от точки минимума производная отрицательна, справа - положительна.
Если же слева и справа от исследуемой точки производная имеет один и тот же знак, то в этой
точке
экстремума нет.
Отметим на рисунке границы отрезка, о котором
идет речь в условии задачи. На этом
отрезке найдем точки, в которых
производная функции обращается в 0 и при переходе через
эти точки
меняет знак. Это и есть точки экстремума функции на отрезке.
Определим, какие из этих
точек являются точками максимума или минимума. Сосчитаем их
количество.
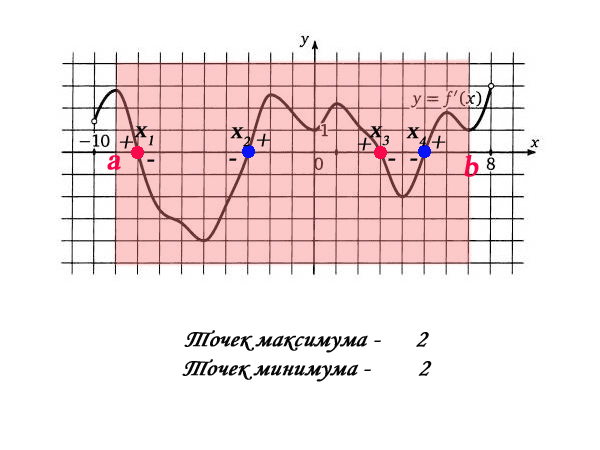Особое внимание здесь стоит обратить на то, что дан именно график производной,
и точки
рассматриваются не на всей области определения, а на конкретном отрезке. Уточнить,
какие именно точки вам следует найти.
|