Теоретический материал к задаче 8 типа
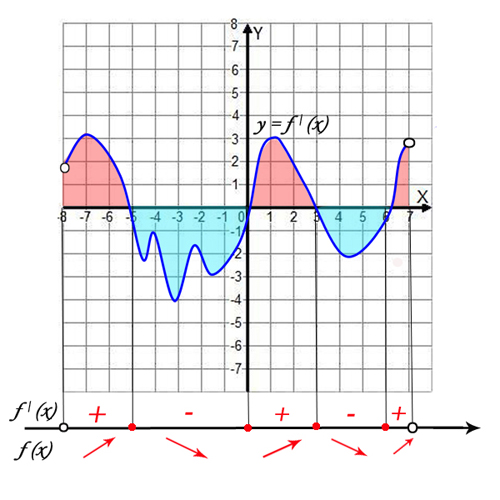
Если функция непрерывна на промежутке Х, и
выполняется неравенство f'(x)> o, то
функциия y=f(x)
возрастает на промежутке Х; если же на промежутке Х выполняется
неравенство
f'(x)< o, то функциия y=f(x) убывает на этом промежутке.
Если f'(x)=0
на промежутке Х, то на этом промежутке
функциия y=f(x) постоянна.
Если функция непрерывна не только на промежутке, но и на его концах, то эти
точки
включаются в промежуток монотонности.
В задаче требутся сначала найти промежутки возрастания (f'(x)> o) или убывания
(f'(x)< o), а затем выбрать из них наибольший или наименьший.
|